Compiler
Why should I learn COMPILER?
There are mainly three reasons:
- curiosity about the essence of programming languages
- willingness to challenge myself through completing a hardcore course
- discovery of potential professional direction in the future
In fact, these reasons are not persuasive enough to motivate me to insist on learning compiler. However, after staying at home for half a year without making much progress, I realized it is essential to at least accomplish something, and hence to learn compiler theory as soon as possible.
I follow the open course of Standford CS143, which aims to design a compiler for a language they invented, called COOL, and my assignments are recorded in a GitHub repo. Additionally, edx provides related courses and materials as an supplement to its official website.
Structure of compiler
A compiler can be divided into five phases:
- lexical analysis
- parsing
- semantic analysis
- optimization
- code generation
It is a clever way to partition the whole process into sperate building blocks, just as dividing a web application into frontend, middle-ware, backend.
Nowadays, optimization becomes the most critical part which was not the case when it was first invented.
Lexical Analysis
It is intuitive to first identify strings that are well-defined and classify them into correct category, which is called lexical analysis. For example, we could identify class as a keyword, "hello" as a string constant. We call this <sub-string, class> pair token.
To successuflly identify tokens from a input stream (usually a file), we usually write specifications (or say patterns) of the token class, and then try to match the input stream with these specifications.
Specification - Regular Expression
How to define a pattern? It is hard to give an concrete answer, while there is an intuition that a pattern can be expressed with some rules described by a program, and hence may be treated by some pure math expressions.
The answer is regular expression, which only contains five elements (two building blocks and three operations):
- single character c
- empty string
- union: A + B =
- concatenation: AB =
- iteration: = , where means concatenate itself for i times (specifically, )
This is really amazing and powerful because it looks like almost any pattern can be described by only these five elements, e.g. any non-negative integer can be expressed as (0+1+2+3+4+5+6+7+8+9)(0+1+2+3+4+5+6+7+8+9)*, which can simply written as [0-9]+.
Match Patterns - Finite Automata
Given an input stream and patterns defined by regular expressions, how can we match substrings with any pattern? It is also amazing that this matching procedure can be translated into a mathematical structure along with its matching algorithm. This structure is called finite automata (FA):
- a set of states S
- a set of actions A (usually it represents any valid characters of an input stream, also denoted as an alphabet )
- a starting state n
- a set of accepted final states
- a transition mapping
To translate a regular expression (RE) into an FA, what we need to do is simply figure out three RE operations’ couterpart in FA. Actually, it is not that difficult to find its counterpart in Nondeterministic FA, and there is also easy translation to help find a deterministic FA (DFA), and hence an algorithm to perform matching on the DFA.
The details are left blank here as I am not perfectly sure about them, while I belive the basic ideas are illustrated above.
Not surprisingly, this seemingly fully automated procedure is implemented by a well-established software, called Lex (flex for C++ and jLex for Java). Therefore, we only need to define the patterns (i.e. regular expression) in Lex and perform simple actions to generate tokens. Then, Lex will help complete the rest parts of the lexical analysis stage.
Lookahead
Example in FORTRAN (as it tries to neglect whitespace)
1DO 5 I = 1,25
2DO 5 I = 1.25Try to minimize lookahead in lexical analysis
Regular languages
regular expressions (syntax) specify regular languages (set of strings)
two base cases: empty (epsilon) and 1-character strings
three compound expressions: union, concatenation, iteration
- At least one: =non-empty set, or simply written as
- Option:
- Range: =’a’+’b’+…+’z’+’A’+…+’Z’
- Excluded range: complement of [a-z] = [^a-z]
How to partition: maximal munch
Which token class to choose: by priority
What if no rule matches: do not occur because we introduce an error token class (and put it in last priority)
Formal languages
meaning mapping (function): many to one
Finite Automata
regular expressions = specification
finite automata = implementation
- an input alphabet
- a finite set of states S
- a start state n
- a set of accepting states
- a set of transitions, in state on inpupt go to state
if end of input and in accepting state ⇒ accept
otherwise ⇒ reject (either stuck or the final state is not accepted)
language of a FA = set of accepted strings
-move: can choose to move to another state without consuming input
Deterministic Finite Automata (DFA):
- No -move
- One transition per input per state
otherwise, NFA
An NFA accepts if some choices lead to an accepting state at the end of the input
NFAs and DFAs recognize the same set of languages — regular languages
DFAs are faster to execute while NFAs are, in general, exponentially smaller
Lexical Specification → Regular expressions → NFA → DFA → table-driven impl of DFA
Regular expression to NFA
build from bottom up, and single character NFA, then three compound expr NFA
NFA to DFA
DFA to Table-driven Impl of DFA
2D table T[i, a] = k where
Parsing
motivation: regular expression is not powerful enough to express all languages (its counterpart — regular language — is one of the simplest language of formal languages)
e.g. it cannot express , i.e. arbitrary nesting structure
so we need to transform tokens into parsing tree
CFG
CFG stands for context-free grammar.
CFG is more powerful than RE?
It contains a set of productions and both terminal and non-terminal. Basically, a CFG describes all possible strings merely consisting of terminals.
a production: , acting like a replacement where left-side non-terminal can be replaced by right-hand side (could be either terminal or non-terminal, and even )
parse tree
CFG specifies whether while we want more, e.g. association of operators, so we need a parse tree for
a derivation (a series of productions) defines a parse tree, while a parse tree could have multiple derivations → ambiguity
how to solve ambiguity? no automatic methods, while we could use precedence and associativity declarations to solve it
error handling
- panic mode: throw away errors until a clear defined tokene.g. means if error occurs it will try to neglect until an integer is found or if the error is closed within parentheses
- error productions: specify common mistakes in grammar, e.g. 5x instead of 5*x goes to the rule . However, this complicates the grammar
abstract syntax tree
leave out redundant information from parse tree, e.g. parentheses and single element edges, and it becomes more efficient and easier to use
parsing algorithms - recursive descent
for each non-terminal, try productions in order, if fails then do backtrack
- a naive implementation will lead to falsely rejection (when a non-terminal is accepted, it has no chance to backtrack)
- left recursion will lead to infinite recursion, e.g. luckily, this can be automatically solved by rewriting it to right recursion like and furthermore, non-immedaite left recursion can also be solved automatically
despite issues above (which however can be solved), it is used by gcc due to its general acceptence on grammar
parsing algorithms - predictive parsing
similar to recursive descent, but without trying productions, only one choice of production
given left-most non-terminal and the next input token, it can identify the unique production (otherwise an error raised), so no backtrack needed
therefore, we can construct a parsing table to lookup the production we need
- restriction on the grammar: LL(k) language, stands for left-to-right scan, left-most derivation, with k-token lookahead, for unique choice of production. In practice, , i.e. only lookahead the next token
- a strategy to convert the grammar to LL(1): left-most non-terminal factorization, e.g. becomes and
first set
follow set
bottom-up parsing
shift-reduce parsing
handle
- to find viable prefixes, which are regular languages, so use FA to find it and corresponding productions for reduction
- SLR grammar, a heuristic to detect handles without conflicts, while not all languages follow SLR grammar, so precedence declarations (or formally speaking, conflict resolutions) are needed
Semantic Analysis
motivation: some language constructs are not context-free (i.e. syntax parsing is not enough)
type checking is the major part of semantic analysis, other checks (most of them are language dependent) include like make sure methods in a class are defined only once
scope: statically scoped and dynamically scoped
symbol table: a data structure to track symbols in current scope
type, static or dynamic types, type checking and inference
inference rules
if A has type T and B has type T then C has type T
where means “it is provable that …”
type environment (because we need information out of the expression): a function from Object Identifiers to Types, , is an assumption over free variables (i.e. the domain is the set of free variables, where free means variables defined out of current expression / its AST node or subtree)
- means we modify our by requiring , which can be implemented by using symbol table
- type environment is passed down the AST, while types are computed bottom-up
In COOL, class and SELF_TYPE are the type
subtyping
, called is a subtype of (by looking at a type tree downwards from the root type), e.g.
In COOL, for all attributes in class
the least upper bound of and is if
In COOL, lub is their least common ancestor in the inheritance tree
typing methods
- we need a seperate mapping for method signatures, where is the class and is the method (notice that previously we define an for object type environment, so we have two TE now)
In COOL, to solve SELF_TYPE issues, we introduce the current class to our TE
type checking is highly customed to languages
static type: detect common errors at compile time (no overhead at runtime), but some correct programs are disallowed, and more expressive type systems are more complex
for COOL, dynamic_type(E) static_type(E)
for COOL, programs like the following will be disallowed
1class A { foo():A { self; }; };
2class B inherits A {};
3b:B <- (new B).foo(); -- error: try to assign a supertype to a subtypeso we need SELF_TYPE, but it is not a dynamic type (but determined at compile time), just a feature to help type checker accept more correct programs
for SELF_TYPE as the declared type of E in class C, i.e. class C { … E:SELF_TYPE …}
dynamic_type(E)
where refers to an occurence of SELF_TYPE in the body of
SELF_TYPE is usually not a component in morden languages but a research idea.
In practice, there should be a balance between complexity of type checking and its expressiveness
error recovery is simpler than that in parsing, but what actions should take after identifying a type error?
- assign type Object to it → cascading errors
- assign type No_Type to it → harder impl as class hierarchy is not a tree, but a solution used in real compilers
The role of front end:
- enforce language definition
- build data structure used for code generation
Runtime Organization
COOL has two assumptions: sequential execution and each procedure will return to the point where its parent calls
activation: execution of a procedure
activation records (or frame): contain information for a procedure to execute
globals: static data stored outside of AR but at a fixed place
heaps: data outlives a procedure, so not stored in AR but on heap
alignment: many machines only accept data with word-alignment, so padding is often used
stack machine: results are stored on top of the stack, operands take arguments from the top
benefits of stack machine vs. register machine: compact code, e.g. in stack machine operand addition is simply an instruction add, while in register machine it becomes add r1,r2,r3, stack machine is used by Java bytecode; but register machine is faster
so, we need a balance: n-register stack machine, which keep the top n locations of the stack machine into registers; a 1-register stack machine is called the accumulator
for an accumulator, only one memory op is required for add, while stack machine needs 3
Code Generation
For COOL, we use MIPS as the hardware to run our code. To simplify the project, we only use a few registers (while MIPS has 32 general registers): $a0, $t1, $sp (points to the next unused stack address), $fp (points to the current activation, i.e. to the top of the frame), $ra (return address). Therefore, we are working on an accumulator (only $a0 is used for long-time storage, $t1 is used temporarily).
When producing codes for expressions, we need to follow two invariants:
- the result of the expression should be kept in $a0
- the stack should be preserved (both $sp and contents)
- keep $sp the same
- do not write to address before the address of $sp when we evaluate the subexpression
For example, the generated code for e1+e2 is
1cgen(e1+e2) =
2 cgen(e1) // result is kept on $a0
3 // store result on the stack, because next action will modify $a0
4 print "sw $a0 0($sp)"
5 print "addiu $sp $sp -4" // $sp is used, so move $sp to the next position
6 cgen(e2)
7 print "lw $t1 4($sp)" // load result of top of the stack, which is $a0
8 print "add $a0 $a0 $t1" // store result of e1+e2 to $a0
9 // recover the stack (as long as there exists a $sp modification, we need to restore it)
10 print "addiu $sp $sp 4"Notice that if we put the result of e1 to a temporary register t1 instead of on the stack, the following evaluation of e2 may pollute the register t1, leading to a wrong result.
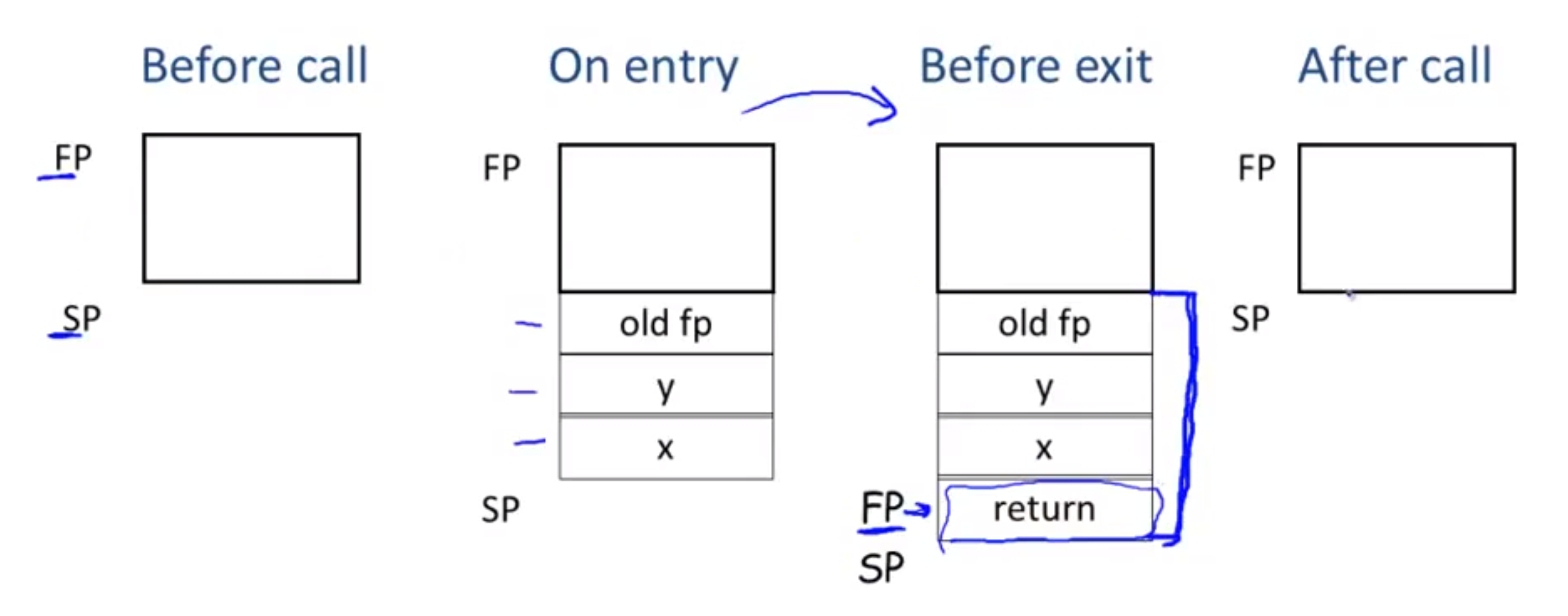
For the function’s generated codes, it should maintain an activation record, which will involve both caller side and callee side codes. (Notice that this part may be complicated, you should be particularly clear about the fact that the stack stores codes and data in separate places, so the picture below only shows how data is stored on the stack; while things like jal reflect movement in code.)
The caller stores its current frame pointer (i.e. old fp), stores all actual parameters, and a return address, then the code jumps to the callee part.
For the callee part, it just begins a new frame (a new procedure), so fp is refreshed. After a function call, everything on the stack should be recovered, just like ending up an expression evaluation, and resumes the old procedure with the return result stored at $a0.
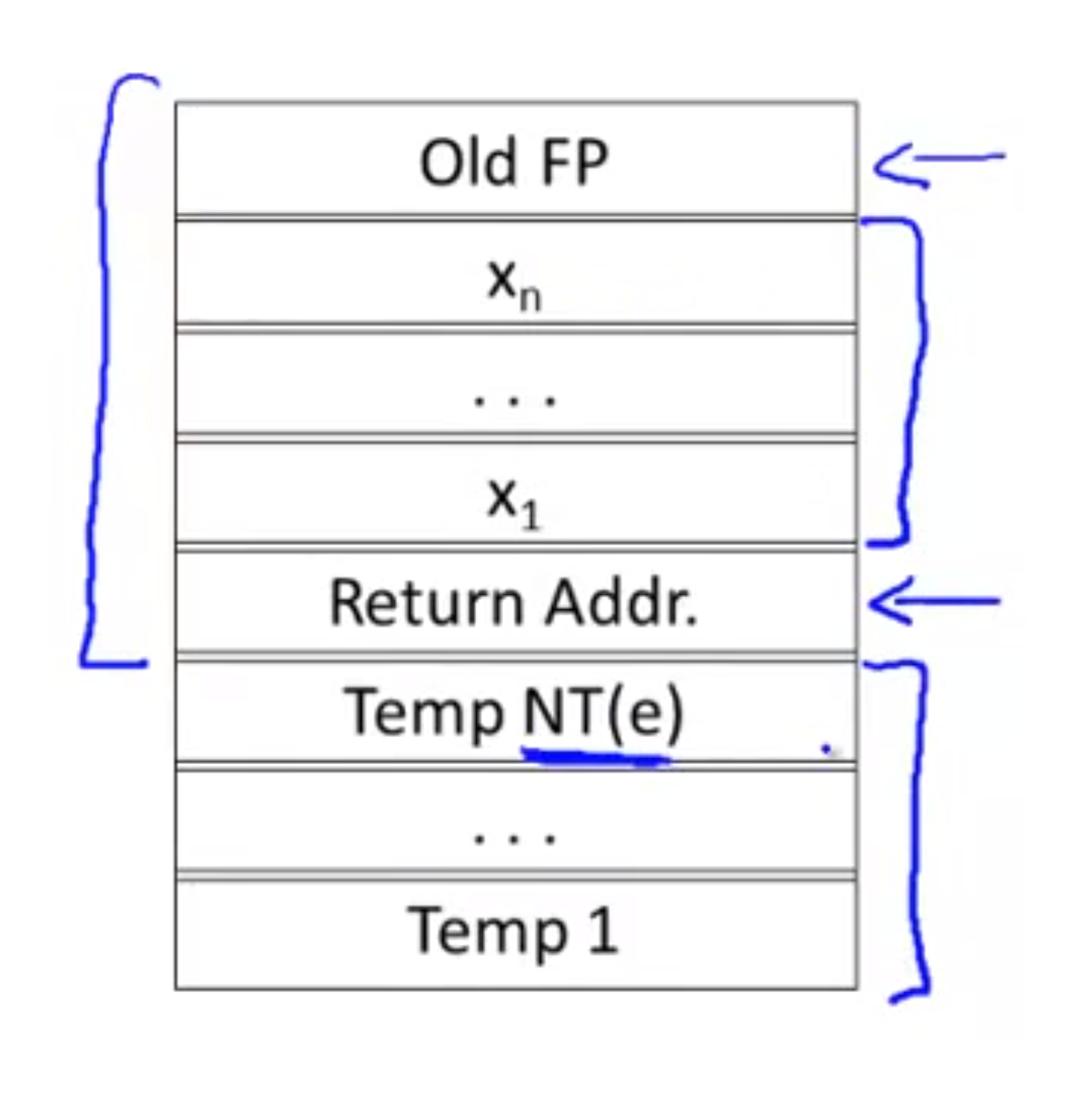
Temporaries
If temporaries are stored in AR (as illustrated above in the cgen(e1+e2) example (though storing them in AR is not as efficient as in registers, it is sometimes the case), to improve the performance, we can know the numbers of temporaries in advance, and thus allocate a fixed size for them. Therefore, we can save the instruction numbers for dynamically allocating places in the AR.
NT(e) = minimal numbers of temporaries need to evaluate an expression e
NT(e) is fixed for an AR, and thus the codegen is improved as
1cgen(e1+e2, nt) =
2 cgen(e1, nt)
3 sw $a0, nt($fp)
4 cgen(e2, nt+4)
5 lw $t1, nt($fp)
6 add $a0, $t1, $a0where nt is used to track the next position of available temporaries. The fixed places to store temporaries can be viewed as a local stack.
Object Layout
One idea to keep in mind is: any code working for class A should always work for any subclass B.
Based on this idea, we can define the layout in such a way: given a layout for class A, a layout for subclass B can be defined by extending the layout of A with additional slots for the additional attributes of B. This leaves the layout of A unchanged.

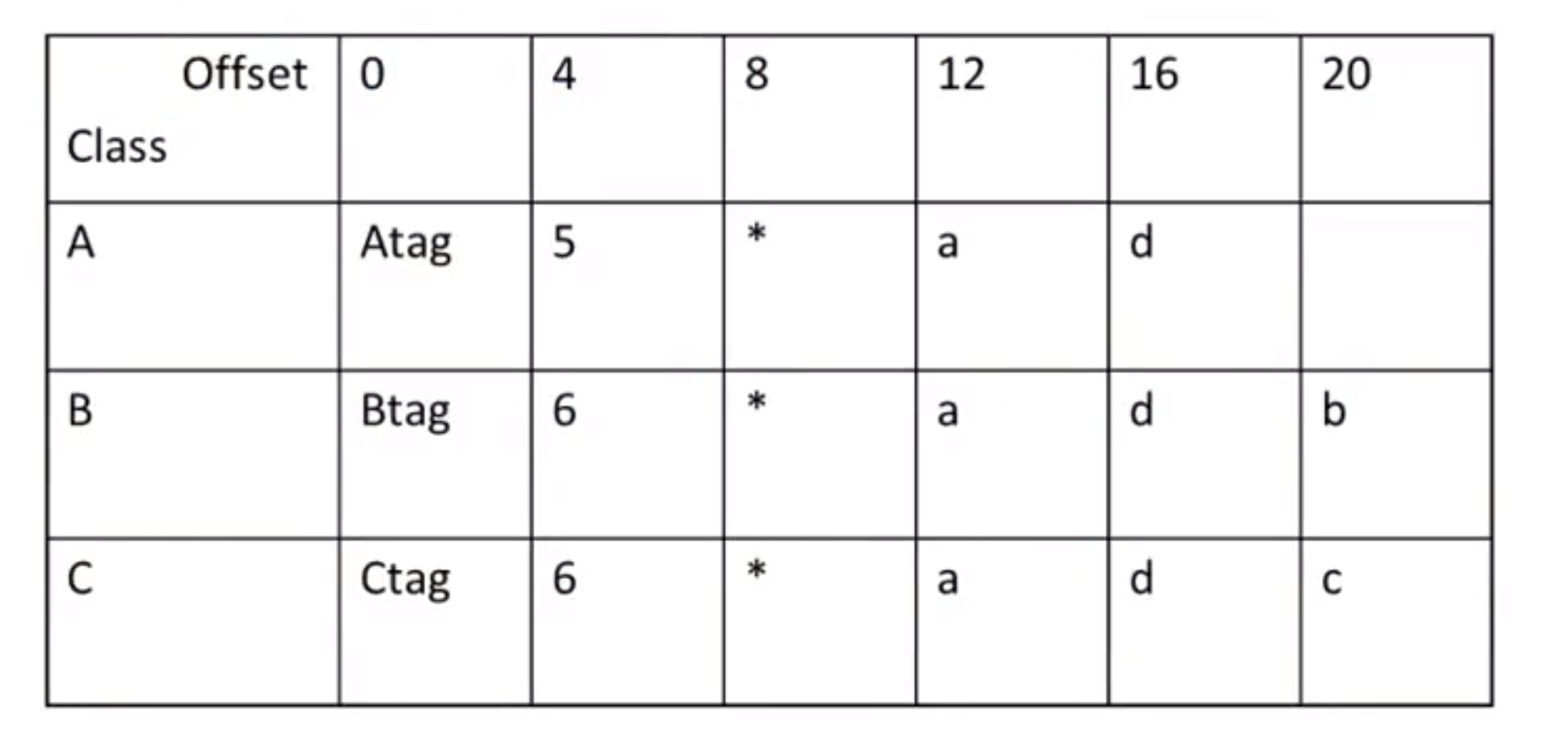
For dynamic dispatch like e.f() where e is of class B and f is both defined in A and its subclass B (an overridden method, since e is of B, f uses this version), we need to identify which method it uses.
The dispatch layout also shares the same offset for those defined in the superclass and in subclasses in case of any overridden.
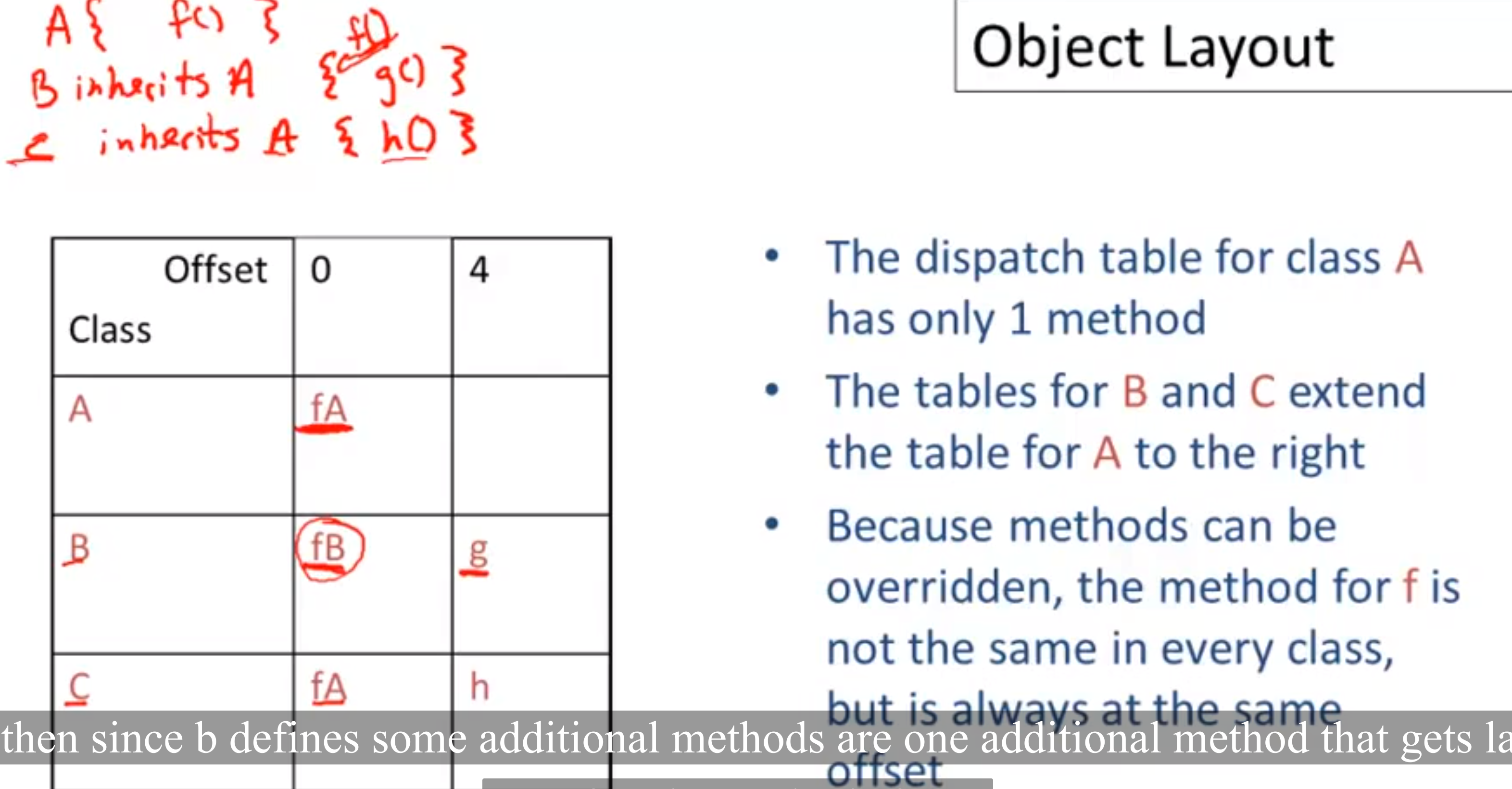
The reason why we have a separate dispatch table is that it can be reused among all instances of the same class, while attributes are not the case.
semantics overview
Denotational semantics: program’s meaning is a mathematical function
Axiomatic semantics: program behavior described via logical formulae (foundation of many program verification systems)
operational semantics
similar to type judgment, formal operational semantics is defined as
We track variables and their values with:
- an environment: where in memory a variable is (a mapping vars → memory locations)
- a store: what is in the memory (a mapping memory location → value)
Thus, a variable environment is defined like , which only tracks variables in scope. A store environment is defined like
Basically, it adds a concept of location.
In COOL, an evaluation judgment is , where so is the current value of self, and this judgment is held for terminating evaluation.
COOL semantics
Intermediate Code
provides an intermediate level of abstraction. there are many IL.
we will look at a high-level assembly
- use an unlimited number of registers
- each instruction is of the form (three-address code)
- x := y op z
- x := op y
- where y and z are either registers or constants
- code to compute the value of e using register t
1igen(e1+e2, t) =
2 igen(e1, t1)
3 igen(e2, t2)
4 t := t1 + t2- unlimited number of registers ⇒ simple code generation
optimization overview
we can classify the codes into basic blocks which is a maximal sequence of instruction with no lable (except for first instruction) or no jump (except for last instruction).
so, we can construct a control-flow graph as a directed graph.
we can optimize / improve the program in:
- execution time
- code size
- network messages sent, memory usage, disk usage, power, etc.
there are three (at least for C and COOL) granularities of optimizations
- local optimizations
- apply to basic blocks
- global optimizations
- apply to a control-flow graph in isolation
- inter-procedural optimizations
- apply across method boundaries
In practice, many fancy optimizations are not implemented since they are hard to implement, costly in compilation time, have low payoff (may reduce the performance). Many fancy optimizations have the property of all three.
goal: maximum benefit for minimum cost
local optimization
remove redundant instructions
simply instructions like algebraic reduction
constant folding: ops on constants can be computed at compile time
- it can be dangerous, e.g. in cross-compiler scenarios where codes compiled on X architecture has a different floating-point round-off strategy from the runtime of Y architecture. this can be solved by storing full-precision strings within compiler on X and let Y to decide how to round off.
eliminate unreachable basic blocks
- it also makes the program run faster because of cache effects and spatial locality
- there are some cases leading to such scenarios, like redundant codes when using a library, results of optimizations, and always-false/true branches.
rewrite intermediate instructions into single-assignment form, where each register occurs on the left-hand side at most once
